When we talked about reaction thermodynamics, we discussed it in terms of Gibbs Free Energy (ΔG°') It would be most convenient to discuss redox reactions in the same units so that we can make a useful comparison. The problem is that when you look up thermodynamics of redox reactions in a book you find them listed in "half reactions" as a reduction potential in VOLTS (E°'). Notice, I wrote "reduction potential. This means that these half reactions are always written in the direction of adding electrons. Before we do anything else. we need to have complete reactions (electron cannot come from nowhere and cannot go nowhere - we must have an origin and a destination) in order to obtain a (ΔE°') in Volts and then thids can finally be converted to ΔG°' in kJ/MOLE!
Shown below are two half reactions for reduction of oxygen and reduction of NAD+. It is very important that the number of electrons in each half reaction are the same so that the addition of the two half reactions balance correctly. In this case both half reactions involve 2 e-. Reduction of molecular oxygen (O2) to 2 H2O is a 4 electron process. Shown below is the E°' for a 2 electron portion so that that it will balance with the 2 electrons in NADH.
| E°' | ||||
| ½O2 + 2H+ + 2 e- | 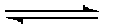 | H2O | +0.82 VOLTS | |
| NAD+ + H+ + 2e- | 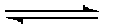| NADH | -0.340 VOLTS | |
Of course what we need to do is transfer electrons from NADH to oxygen. These are both written in the reduction direction (adding e-), If these are added together we will end up with all 4 electrons on one side. This is not what we want - we need the electrons to cancel out. One must be reducing and the other must be oxidizing. In this case, the bottom reaction is backward relative to what we need to do, but the top one is in the right direction
.All we need to do is invert the second reaction When you do this you MUST reverse the sign if the E°'.... After we do this and add the two reactions and cancel out those items that are exactly the same on both sides (and we can also add the E°') together we get a total reaction that is equal to what we want. (and the proper ΔE°' associated with the complete reaction.
| E°' | ||||
| ½O2 + 2H+ + 2 e- | 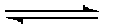| H2O | + 0.82 VOLTS | |
| NADH | 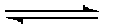| NAD+ + H+ + 2e- | + 0.340 VOLTS | |
| ½O2 + NADH + H+ | 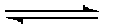| H2O + NAD+ | ΔE°' = + 1.16 VOLTS | |
The ΔE°' is in volts and needs to be converted to kJ/M, but this is easy.... one simple fudge factor called the Faraday constant and a correction for the number of electrons transferred at one time.
ΔG°' = -nF(ΔE°') ....
where n = # of electrons transferred (in this case 2) and
F = Faraday constant = 95.6 kJ/Mole* VOLT
ΔG°' = -2 * 95.6 * 1.16 VOLTS = -221 kJ/M !
for every pair of electrons transferred from NADH to O2.
The ΔG°' for the condensation reaction: ADP + PO4=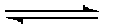ATP = 31 kJ/Mole.
This means that theoretically at least there is enough energy in EVERY pair of electrons to drive the synthesis of about 7 ATP.
We of course do not approach the the theoretical maximum.